一次 関数 と 方程式 133070

一次関数 二元一次方程式をグラフにする2つの書き方 Qikeru 学びを楽しくわかりやすく

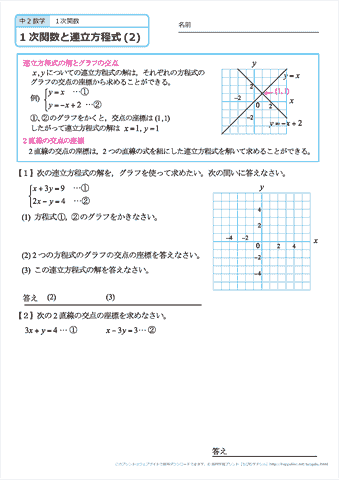
 ①'と②'をグラフにして交点を求める。 ステップ3 グラフから交点を読み取る グラフから交点を読み取る！ グラフの交点が、それが連立方程式の解となるので、解は （x、y）＝（1、2） ・・・（答え） はい、次の問題 中2数学：一次関数と方程式（2Y = 2x 7 のような線形方程式はグラフにすると，直線なので「線形」と呼ばれます。これらのチュートリアルでは，線形の関係，そのグラフ，関数について習います。

一次 関数 と 方程式

一次 関数 と 方程式- 一次とは簡単にいうと わからない文字の部分が一乗になっているという意味です。 一乗の場合には、省略して表すのが普通なので見た目は このようになっています。 もしも、次のように二乗になっていれば これは二次方程式といいます。 もちろん一次方程式とは，その式の中でいちばん次数の高い項が一次だ，ということです。 ニ次方程式なら，その式の中でいちばん次数の高い項がニ次だ，ということです。 ① 4x － 3 ＝ 9 は，xという1種類だけの文字を使っているので， 「一元一次方程式」 ② 5x ＋ 2y ＝ 14 は，xとyの2種類の文字を使っているので， 「二元一次方程式」 ③ 3a － 7b ＝ －9c ＋ 8 は，aとbとcの3種類の文字を使ってい

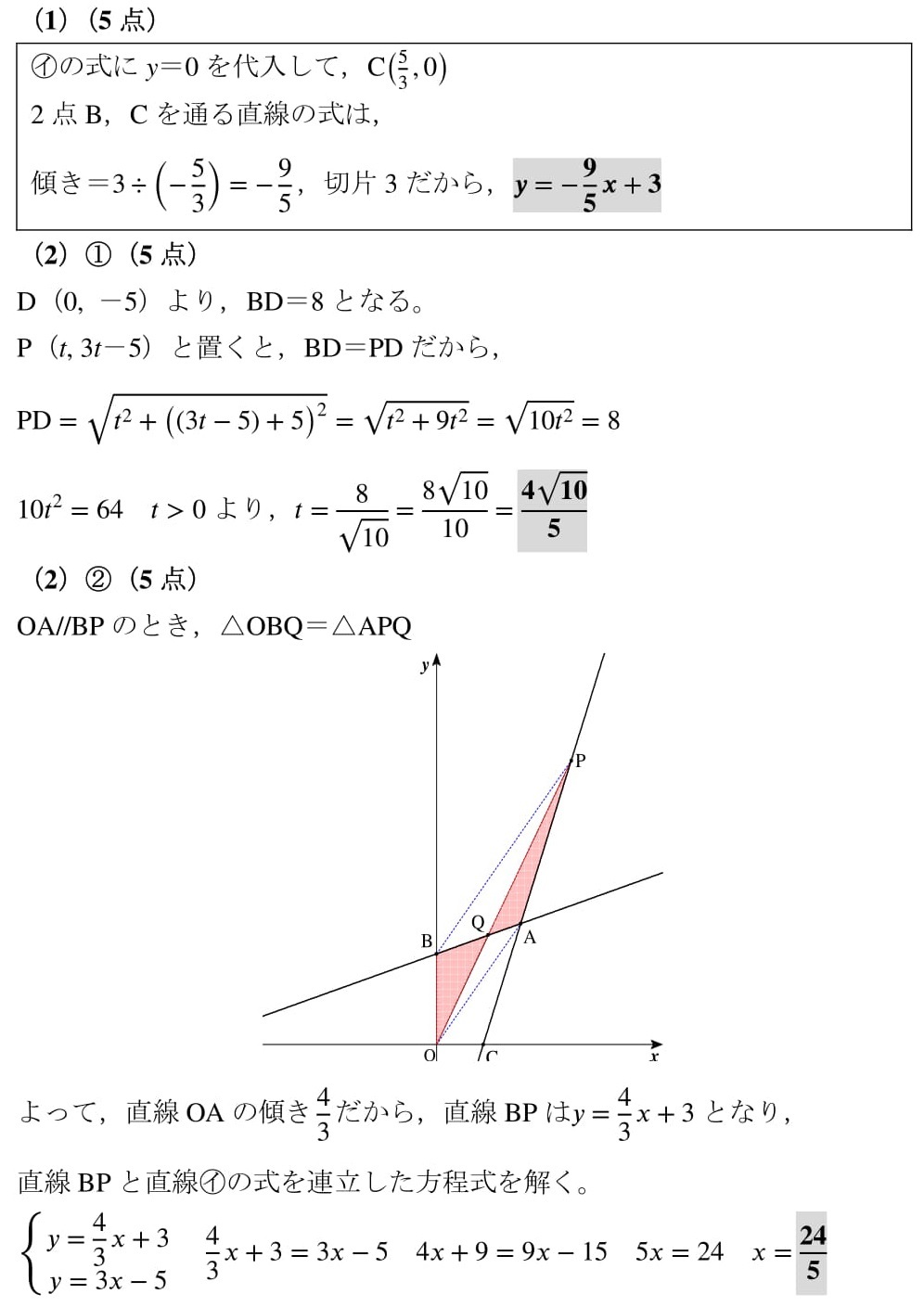
1次関数のグラフの応用 3種類の交点とグラフ上の面積 教遊者

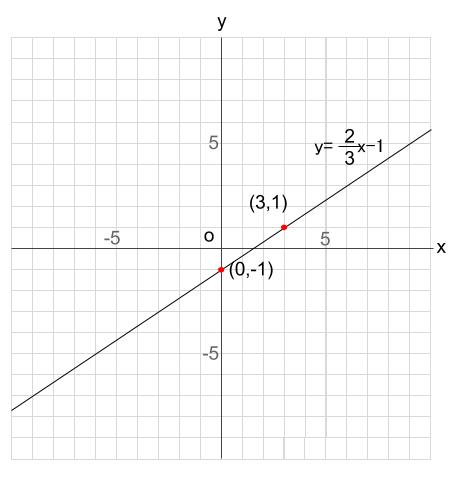
1次関数の方程式 (問題) 次の1次関数の方程式を求めなさい． 1 / 12 点 (2，8) を通り，傾き 6 の直線の方程式 (答案) 求める1次関数の方程式を y = ax b とおくと， 傾きが 6 だから， nnnnnnnnnna = 6 したがって， nnnnnnnnnny = 6x b一次方程式 (一元一次方程式) ア 方程式などの意味 「 方程式 (ほうていしき)」・・・何か言葉だけで威圧されてしまいますね。 ですが、構える必要は全くないです。 順を追って説明しますね 《 例 》 3x2=8 という式があるとします。 一次関数の式「y = ax b」に傾き「a」と切片「b」の値を代入するだけだよ。 例題での「傾き」と「切片」は、 傾き： 5 切片：7 だね。 だから、一次関数の直線の式は、 y = 5x 7 になる。 代入すればいいだけだから簡単だね^^ パターン2 「傾き」と「座標」がわかってる場合 つぎは「傾き」と「座標」がわかっている場合だ。 たとえばつぎのような問題だね。 例題 yはxの一次関

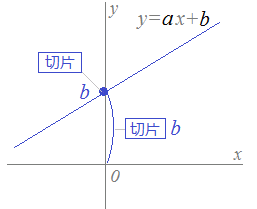
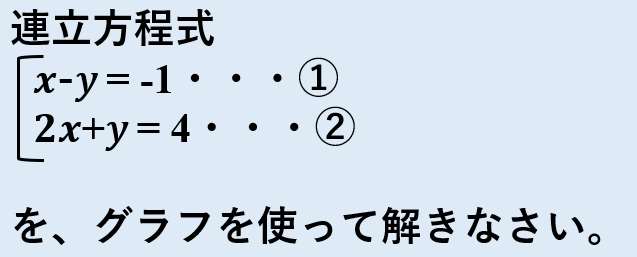
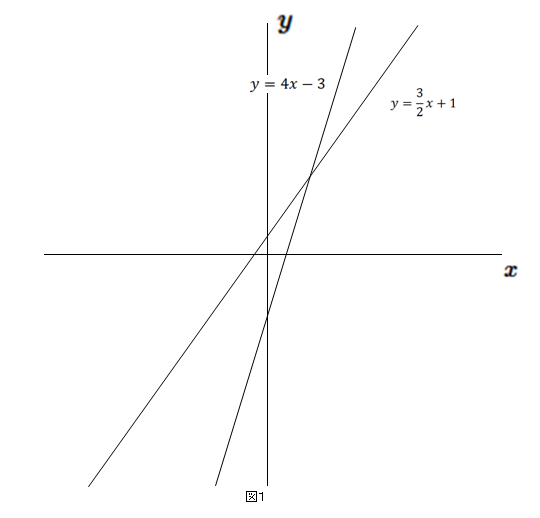
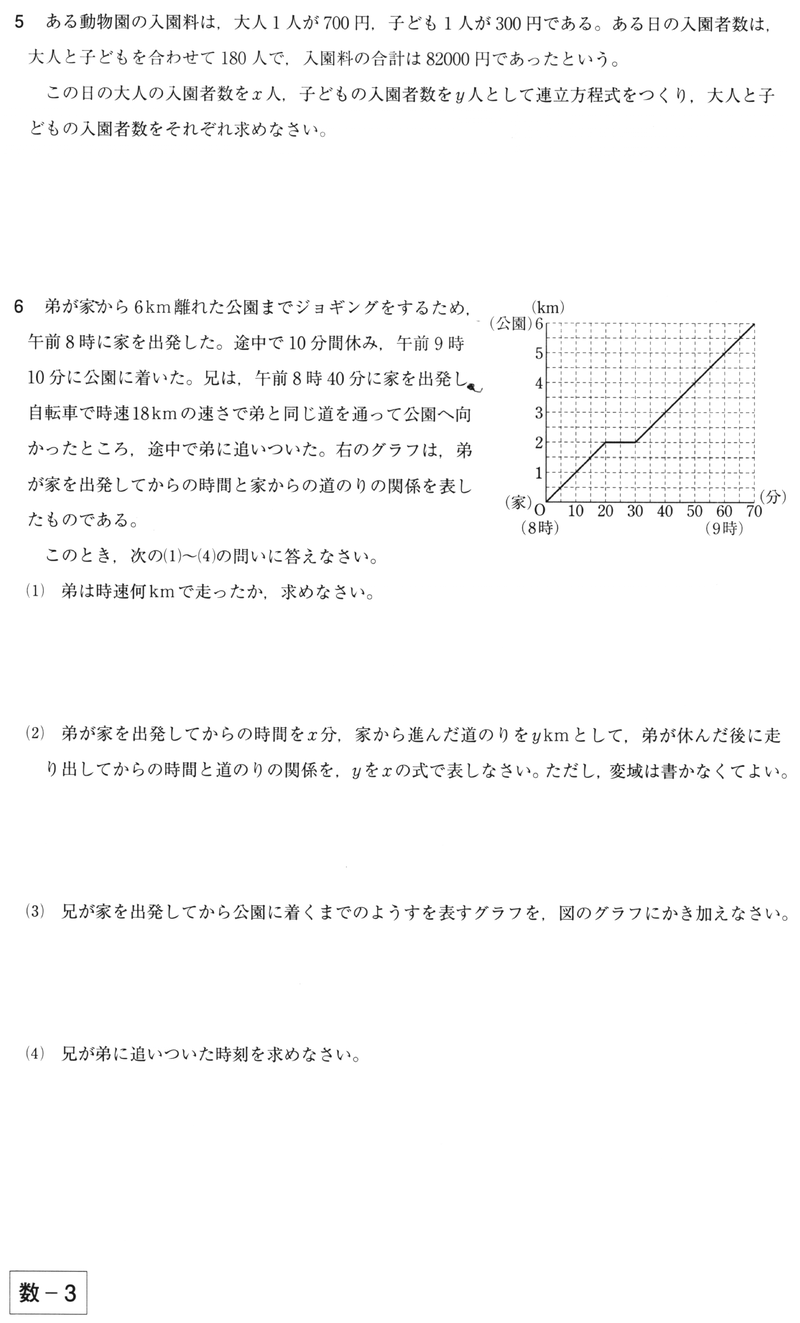
一次関数の式に を代入して計算していきましょう。 すると、交点の 座標を求めることができるので 軸との交点は 座標 とすることができます。 また、一次関数の式 の 部分を見ることですぐに求めることもできます。 軸との交点の座標の求め方 次の一次関数の 軸との交点を求めなさい。 軸との交点、それは言い換えると 座標が0の場所だ！ ということなので、一次関数の式 に を代入しましょう1次関数 1次関数との交点の座標の求め方と、グラフから読み取り直線の方程式を求める方法です。 ここでは一次関数に限定して直線と直線の交点を求める問題を取り上げて説明します。 交点を求める問題は1次関数だけでなく高校の数学でも必ず必要に第6節 1次関数と方程式 ☆ 1次関数は式を用いて表されました。同じように式を用いるものとして方程式を学習し ました。ここでは関数と方程式の関わりについて調べていきましょう。 （1）2元1次方程式 2元1次方程式 2xy=7 で、xが次の値のときにyの値を求め

一次 関数 と 方程式のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

一次関数 式の求め方をパターン別に問題解説 数スタ	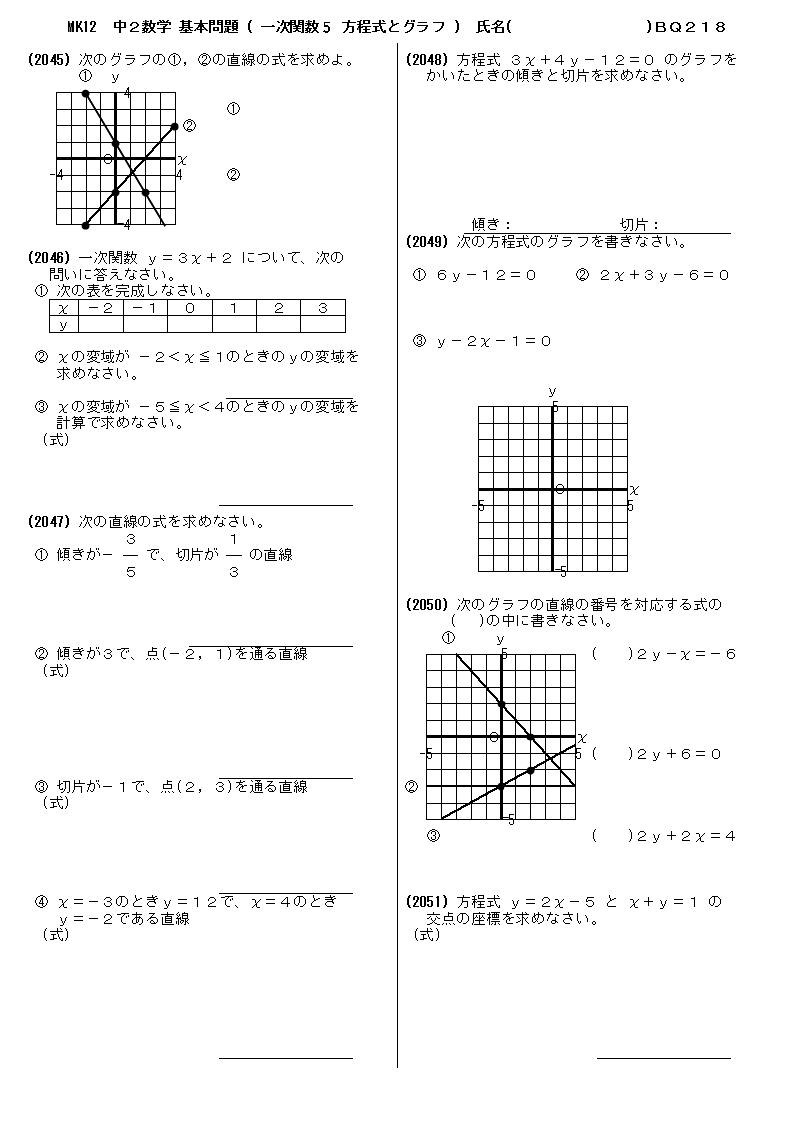一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ	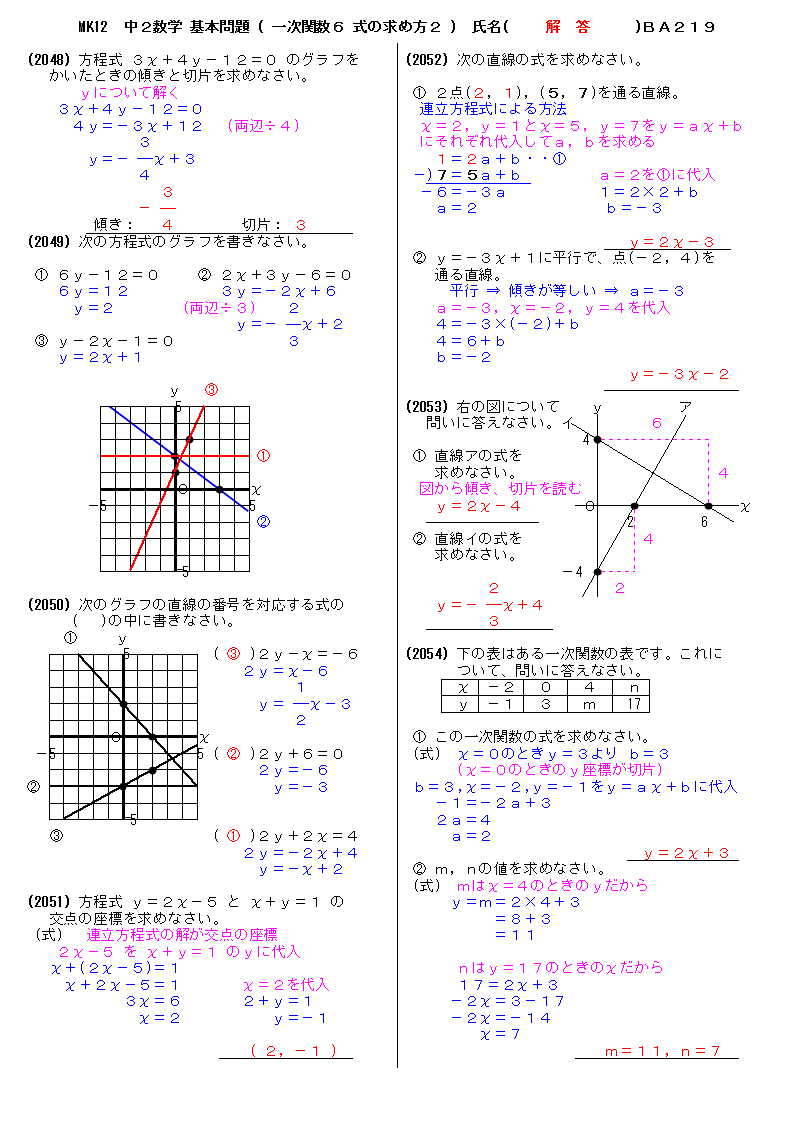一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	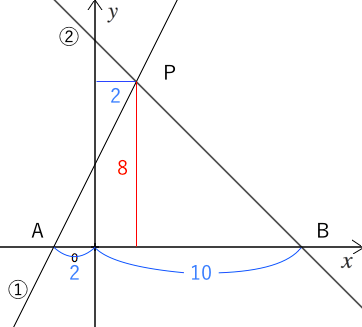一次関数 式の求め方をパターン別に問題解説 数スタ	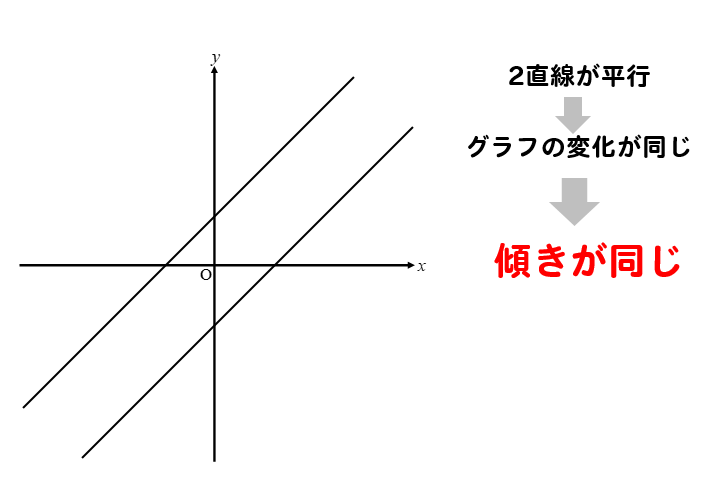一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ	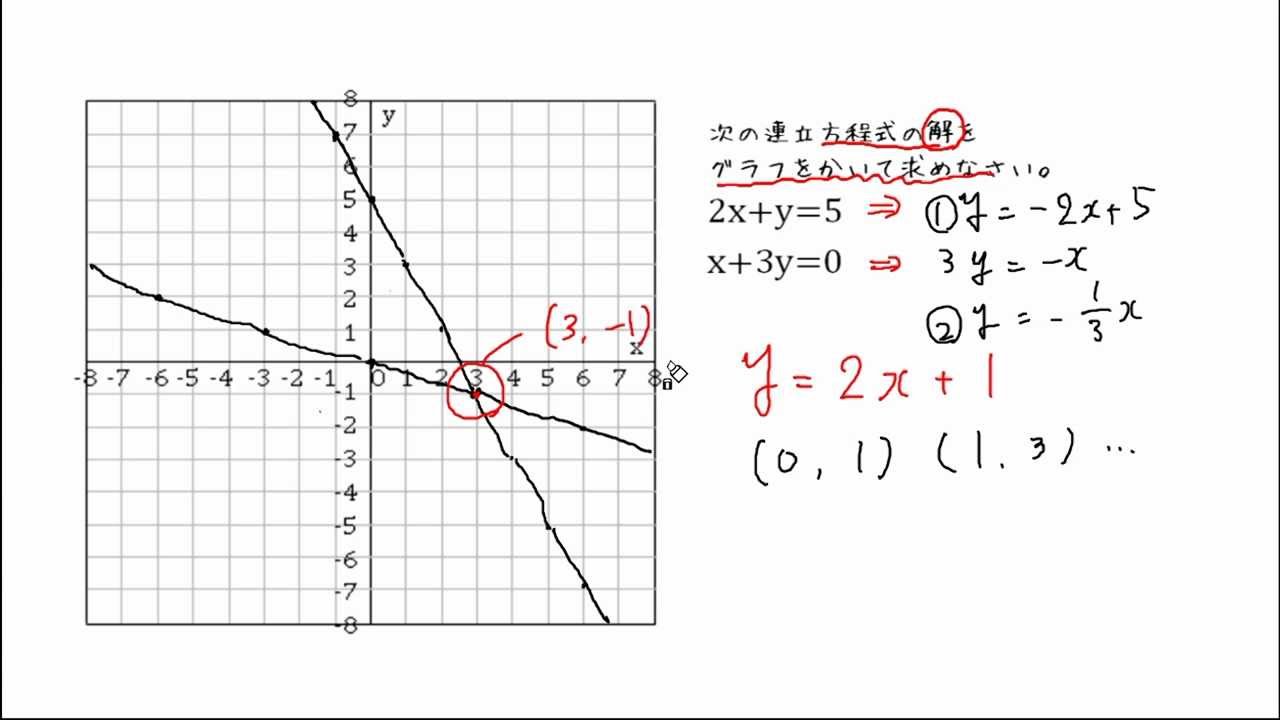一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	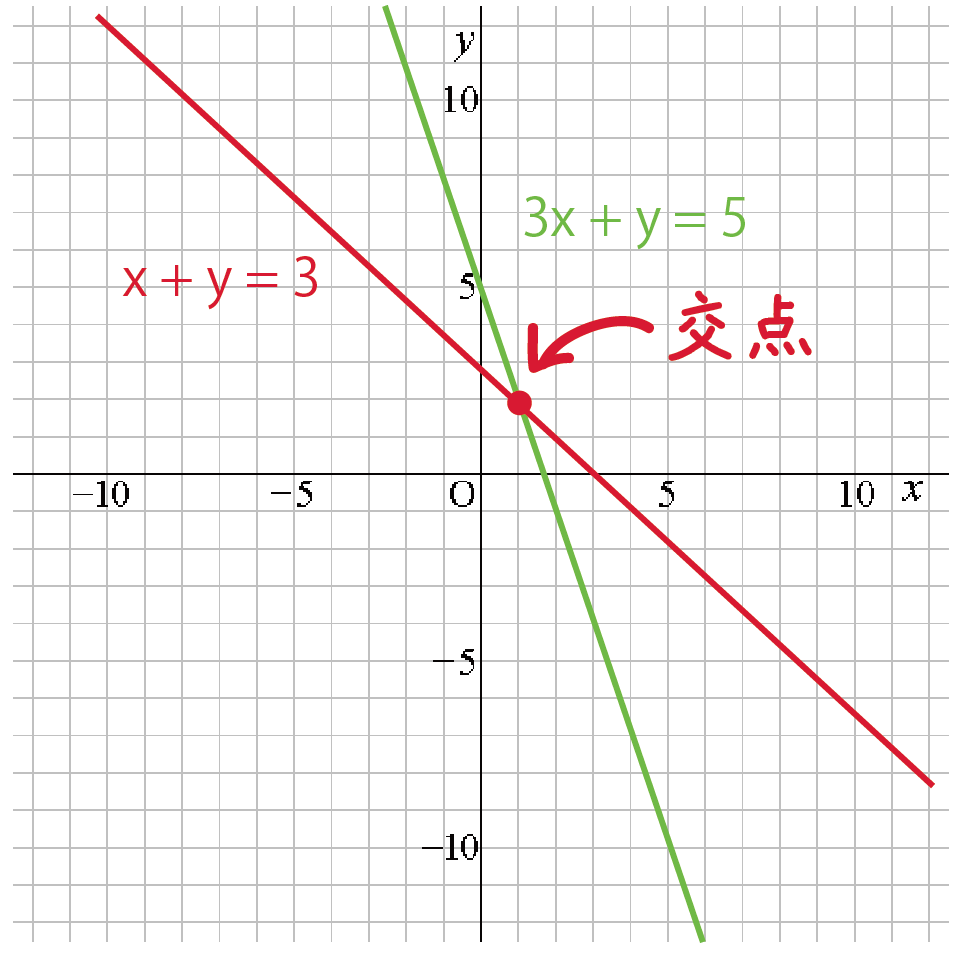一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ	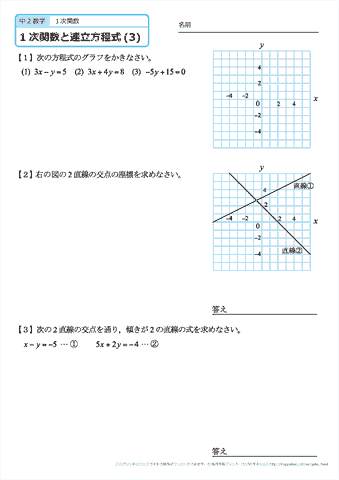一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ	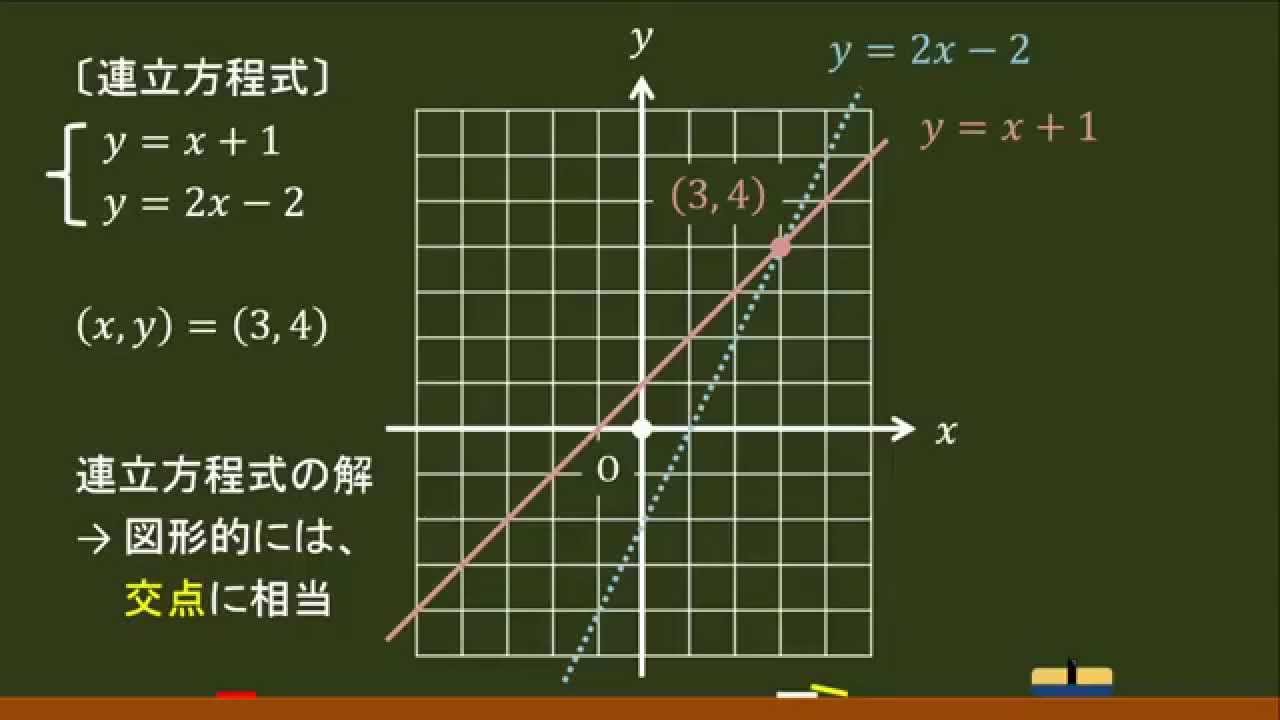一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	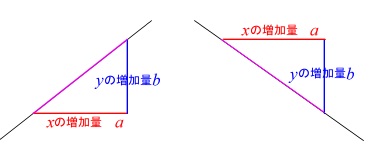一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	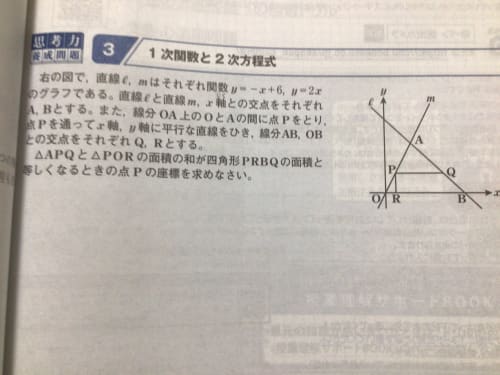一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	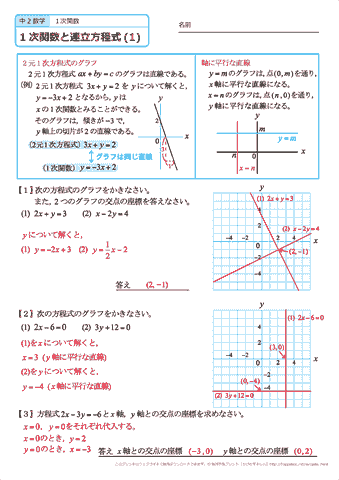一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	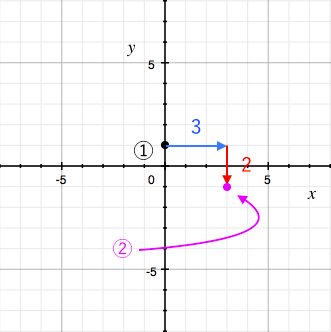一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ	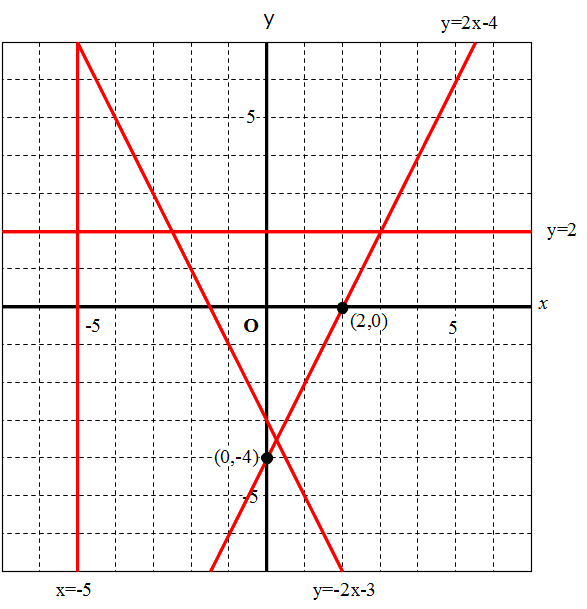一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	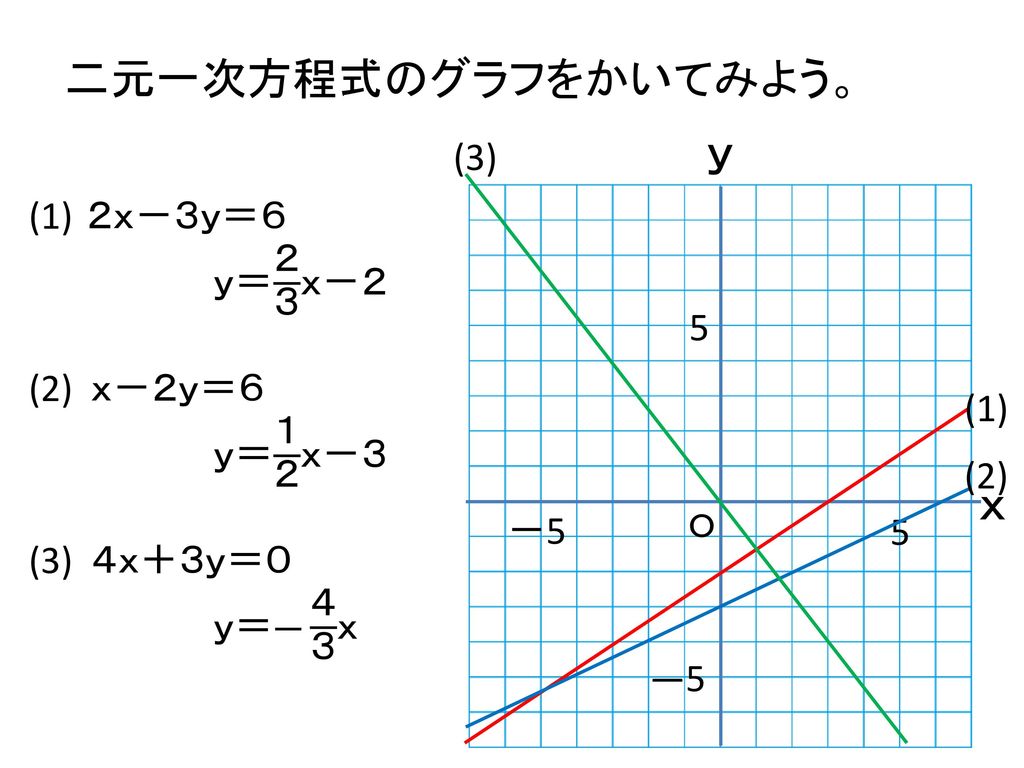一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	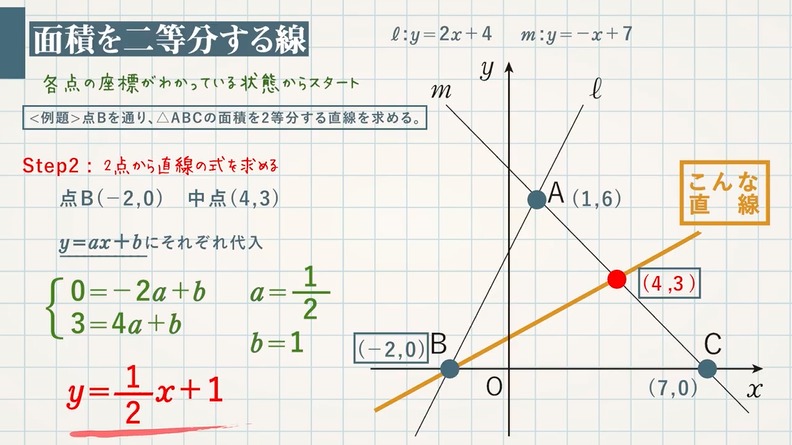一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	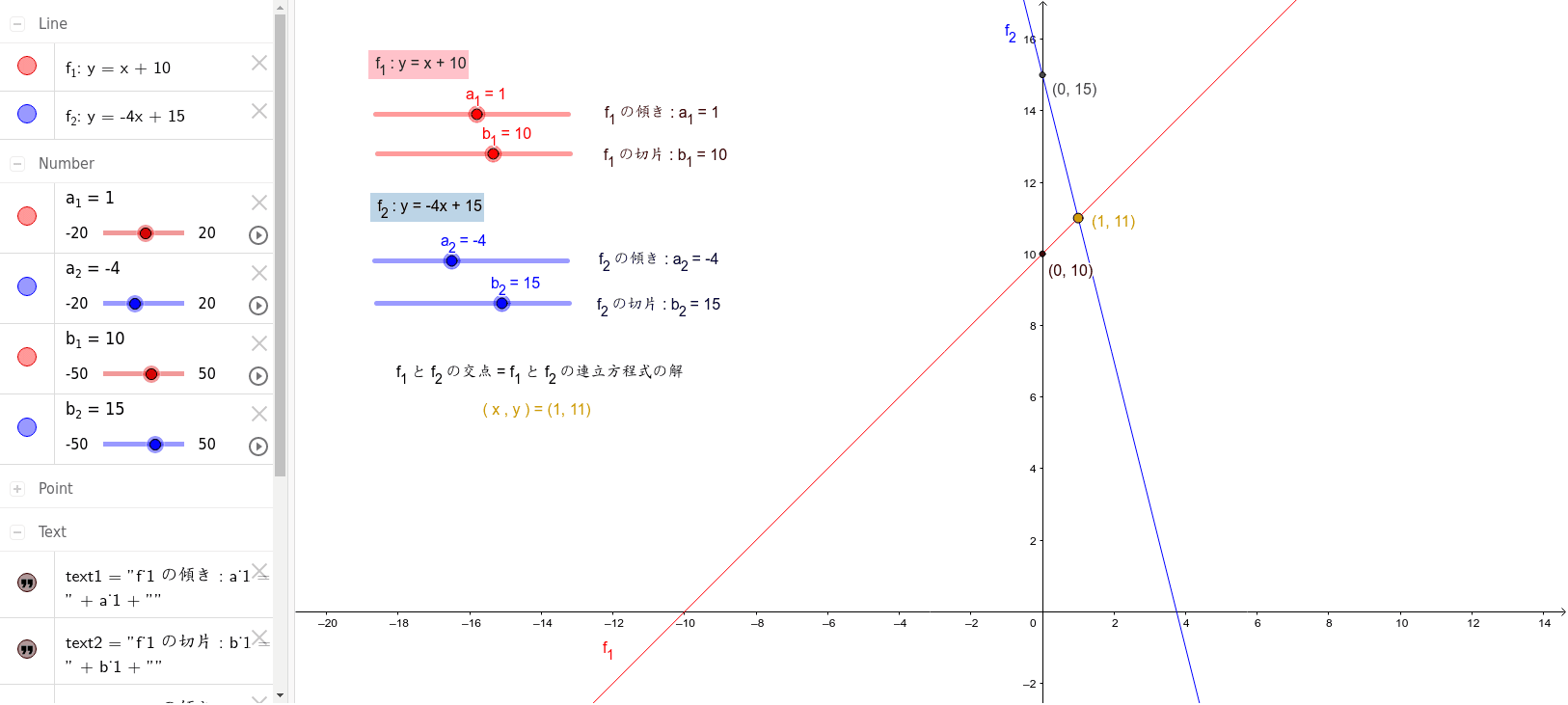一次関数 式の求め方をパターン別に問題解説 数スタ	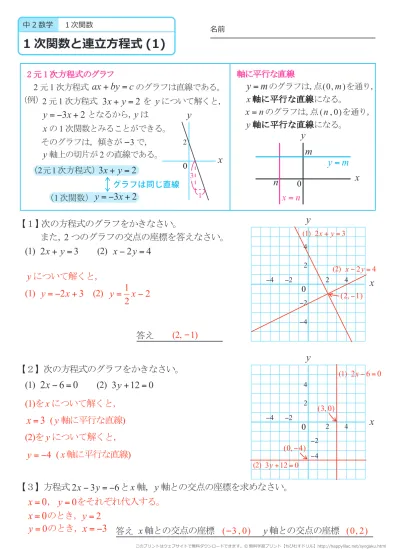一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ	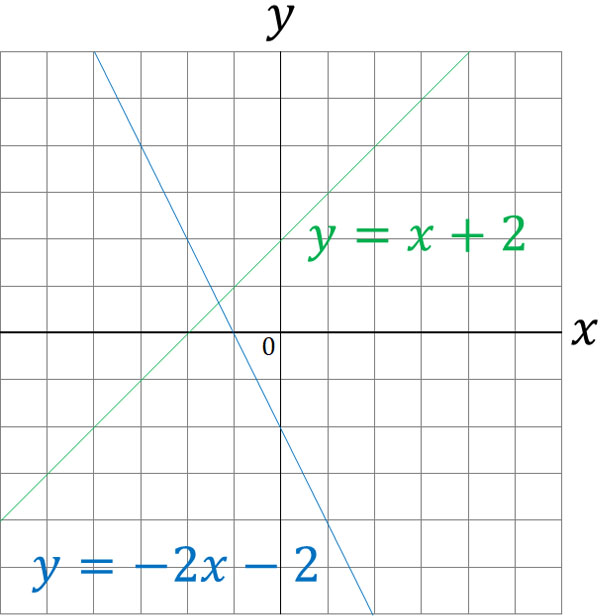一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ	一次関数 式の求め方をパターン別に問題解説 数スタ
一次関数 式の求め方をパターン別に問題解説 数スタ

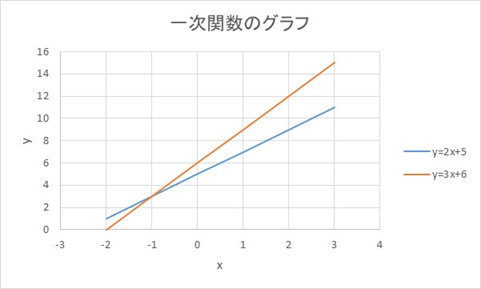
定義と簡単な説明 初等解析学において、不定元 x に関する高々一次の多項式 ax b （ a, b は実 定数）に対し、 x を実変数とみて得られる写像 ,; 一次関数とはずばり、 y = ax b という形をした関数のことさ。 もう少しわかりやすく説明すると、 xが1回以下だけかけられた関数のこと なんだ。 yの右側がxの 一次式 ならそいつは一次関数ってわけさ。 たとえば、 y = 9x とか、 y = 9000x 100 が一次関数になるよ。 だって、y = ax bの形になっているし、xの項はすべて1次式だからね。 これさえ覚えておけば大丈夫。 一次関数